2 Digital Image Fundamentals
Those who wish to succeed must ask the right preliminary questions —— Aristotle
Preview
本章的第一个目的是向你介绍数字图像处理中的一些基础概念,它们将在本书中沿用。
- section 2.1:人类视觉系统的机理,包括人眼成像、光线适应性和辨别能力。
- section 2.2:光以及其他电磁波谱的组成部分,它们的成像特性。
- section 2.3:图像传感器和它们如何成像。
- section 2.4:均匀图像采样和灰度量化的一些概念。
- section 2.5:处理了各式各样的像素之间的基本关系。
- section 2.6:介绍本书中主要使用的数学工具。
第二个目的是帮助你建立一种 "感觉",其关于如何使用这些工具去完成各种各样的基础图像处理任务。工具的范围和用法亦将随后文而扩展。
2.1 Elements of Visual Perception
虽然数字图像处理是建立在数学和概率公式的基础上,但选择合适的技术仍需要人的直觉和分析,而这些选择通常基于主观的视觉判断上。所以本书选择从建立一个对人类视觉感知的基础的理解开始。
由于篇幅有限不可能讲太细。我们的兴趣主要集中在与人类生成图像并感知相关的机理和参数,以及通过一些因素来学习人类视觉的物理限制,它们也同样用于数字图像的处理。
2.1.1 Structure of the Human Eye
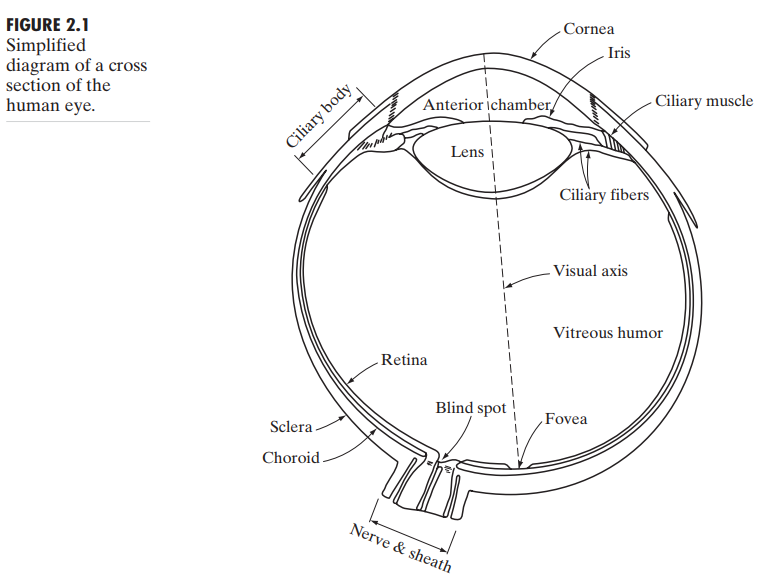
图2.1是一个简化版的人眼横截面图。眼球近似一个球,大约 20 mm 的平均直径。有三层薄膜包围眼球:cornea(眼角膜),sclera (巩膜)外壳,choroid(脉络膜),retina(视网膜)。
cornea 是一种硬而透明的组织,覆盖着眼睛的前表面。与 cornea 相连的是 sclera ,一层不透明的膜覆眼球的剩余区域。
choroid 在 sclera 的正下方,这层膜包含了血管网络,作为滋养眼球的主要来源。choroid 在最前端分为ciliary body(睫状体) 和 iris(虹膜),后者通过收缩和扩张来控制进入眼球光线的数量。
lens(晶状体)由纤维细胞的同心层构成,通过依附于ciliary body 的 ciliary fibers 悬浮。
眼睛最里面的膜是 retina,它布满了整个眼球后部。当人眼适当聚焦,来自外部物体的光线将在其上成像。图像由 retina 上离散的光线接收器提供。接收器主要分两种:cones(锥状体) 和 rods(杆状体)。
cones 的数量在600-700万之间,主要位于视网膜的中间部分 fovea(中央凹),其对颜色高度敏感。人们主要通过它们来分辨图像细节,因为每一个 cones 都连着自己的神经末端。
rods 的数量大约7500-15000万,分布在 retina 表面,它们与彩色视觉无关,而对低照明度敏感。它们用来给出视野内的一般的总体的图像。
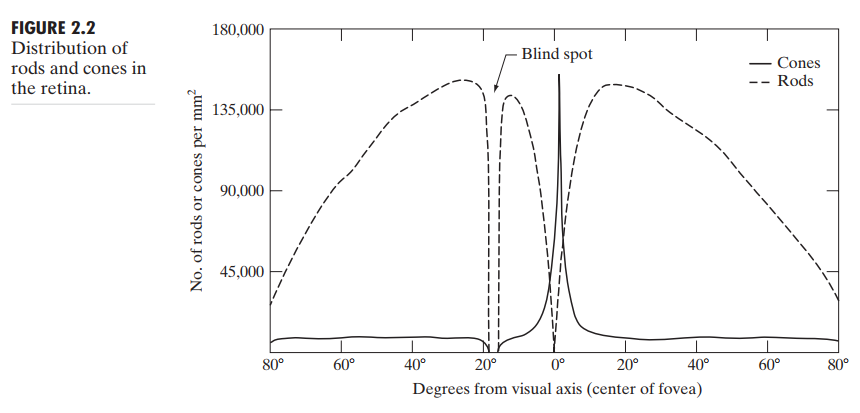
图2.2显示了右眼横截面中视神经出现区域的 rods 和 cons 的密度。可以注意到,cons 的密度从 fovea 往外由大变小,而 rods 的密度先变大后变小,距视轴20°左右最大。当然除盲点外。
fovea 本身是一个直径 1.5 mm 的圆形凹槽,为了便于讨论,我们将它视为 $1.5mm * 1.5mm$ 的方形传感器阵列。其上 cons 的密度大约 $150000 mm^2$,即眼球中最敏锐的区域有大约 33700 个。从自然分辨能力上讲,一个 电荷耦合器(charge-coupled device)成像芯片可以有如此多的传感器在$5mm*5mm$的阵列中。 简而言之,眼睛在分辨细节上的基础能力和现在的电子成像传感器相当。
2.1.2 Image Formation in the Eye
普通摄影相机中,镜头有固定的焦距聚焦不同的距离是通过变化镜头和成像平面的的距离实现的,成像平面即胶片所在的位置。人眼则相反,镜头和成像区域(retina)的距离是固定的,合适的聚焦距离由改变晶状体(lens)的形状得到。这个操作由睫状体(ciliary body)完成,根据目标距离的远近扁平或加厚晶状体。
2.1.3 Brightness Adaptation and Discrimination
Brightness Adaptation
由于数字图像被显示为一个离散的灰度集合。人眼对不同灰度等级的分辨能力在展示图像处理的成果上很重要。人眼视觉系统可接受的光强度的范围很大,从暗示阈值(scotopic threshold)到强光极限(glare limit)。实验数据指出,入射光强度和主观亮度(subjective brightness)是对数函数关系。
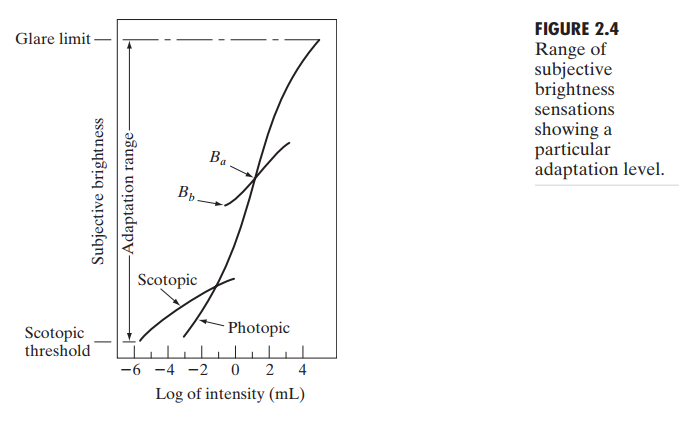
图2.4即 光强-主观亮度图。长实线代表了被视觉系统接受的光强度。亮视觉(photopic)范围大约$10^6$。由暗视觉(scotopic)转变为亮视觉的范围大约是 0.001mL 至 0.1mL(millilambert)。
对图中动态范围的解释中,最关键的一点在于视觉系统不能在一个范围中同时工作,即同时只能适应于某一点的光强。它通过改变整体的敏感性来实现这么大范围的适应性改变,即亮度适应现象(brightness adaption)。眼睛可同时辨别的亮度范围较整个适应范围来说很小。对任意给定的条件集,视觉系统的当前感光等级被称为亮度适应等级(brightness adaption level),例如图中点$B_a$。短斜线表示人眼适应于这个亮度等级下时,主观亮度的范围,低于$B_b$的光将成为不可辨别的黑色,斜线上端实际上没有限制,但是更高强度的光会将亮度适应等级提高。
Brightness Discrimination
关于人眼在某一个特定适应等级下,对光强的变化的辨别能力,一个著名的实验:对象注视一个足够大的充满视野的均匀发光区,这个区域是典型的漫反射体,使用强度$I$的可变光源从后照射它。在其中心的小圆形范围内增加强度为$\Delta I$的闪光。
如果$\Delta I$不够亮,对象说"no",最终加到够亮对象会一直说"yes"。分量$\Delta I_c/I$被称为(Weber ratio),其中$\Delta I_c$是背景为$I$时可辨别照明度增加量的$50\%$。$\Delta I_c/I$越小代表可辨别度越好。
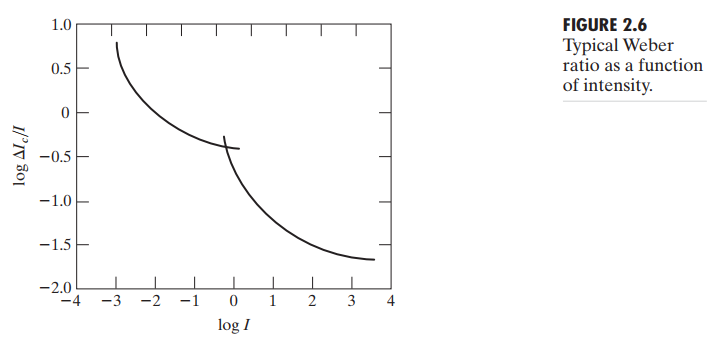
图 2.6 显示,低照明度情况下辨别能力弱,但其随着背景光照增强而迅速增强。两条曲线反映出在低照明度下视觉主要由 rods 提供,而高等级下由 cones 提供。
如果背景光强度固定,且用其他光源代替闪光,将其强度从不能被觉察逐渐变化到始终被察觉,典型的观察者可以观察到 24 次不同的强度变化。粗略地看,这个结果和一个人一张单色图像的任意一点能观察到的不同灰度数量相关。但并不是说一张图象可以被表示为这么点灰度,因为当人眼扫图片时,平均背景发生了变化,故允许在新的适应等级上察觉到不同的强度增量集。最终结果是在整体灰度辩别上眼睛能适应更宽的范围。
summary
这两个现象证明被感知的亮度不是简单的关于强度的函数。第一个现象基于一个事实,视觉系统倾向于在不同光强度的边界产生"下冲"或"上冲"现象,如图 2.7。这样带圆齿的带被称为 Mach bands
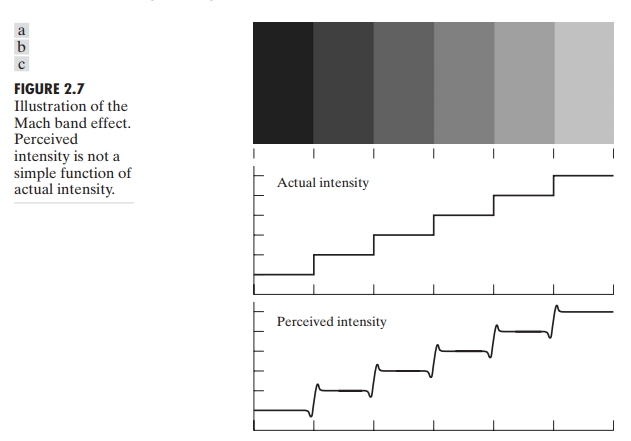
第二个现象被称为 simultaneous contrast ,基于一个事实,一个区域可观察到的亮度不简单取决于其灰度,如图 2.8。

另一些人类感知现象是视觉错觉,眼睛填充了不存在的信息或错误地赶制了物体的几何特性,如图 2.9。
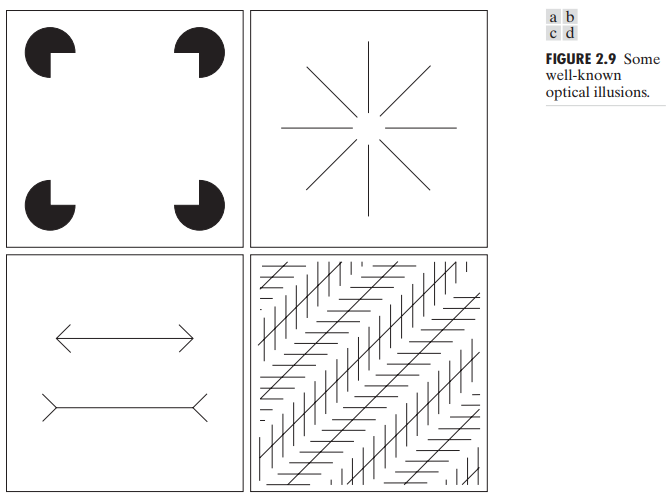
2.2 Light and the Electromagnetic Spectrum
这部分内容与中学相仿。
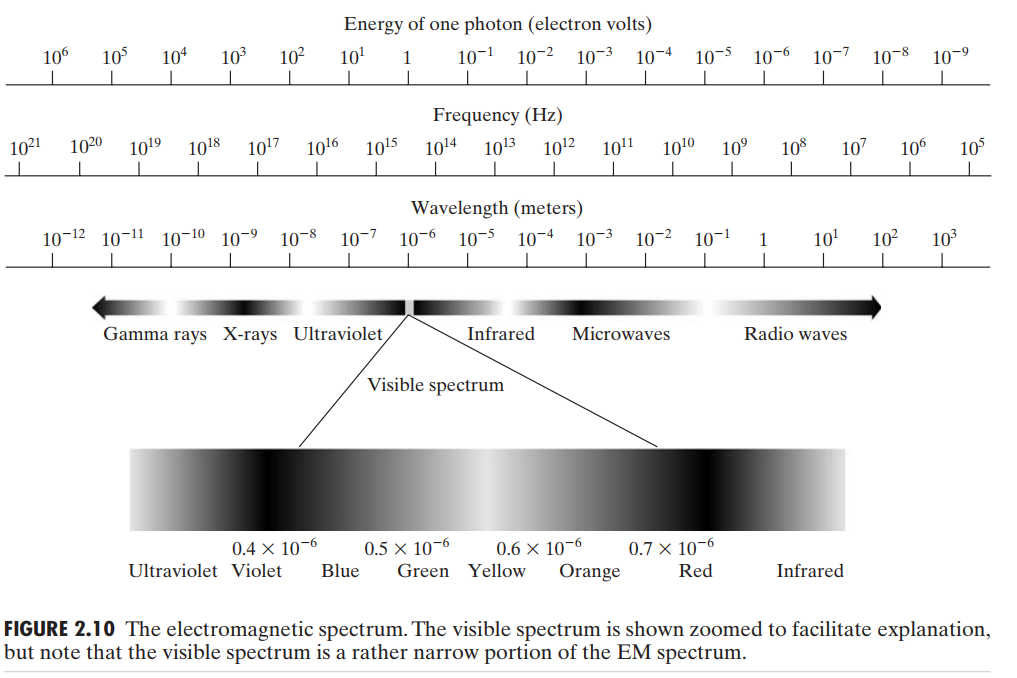
没有颜色的光被称为 monochromatic light(单色光)或 achromatic light(无色光)。单色光唯一的属性是intensity(强度)或大小。由于单色光的强度反映在感知中是从黑色到灰色,最后变成白色的变化,故单色光的强度通常由 gray level(灰度)来表示。我们将在后续的讨论中交替使用术语 intensity 和 gray level。单色光由黑到白时强度测量值的范围被称为 gray scale,而单色图像通常被成为 gray-scale images。
chromatic light(有色光)跨越电磁波谱的大约 $0.43$ 到 $0.79 \mu m$。除了频率,还有三个基本量用来描述有色光的质量:radiance(发光强度),luminance(光通量),brightness(亮度)。radiance 是光源流出的总能量,通常用 watts(W,瓦特)表示。luminance 由 lumens(lm,流明数)度量,表示对象可感知到的光源发出的总能量。brightness 是一种光感知的主观的描述符,不能测量,它体现了光强度的无色概念,是描述色彩感知的重要因素之一。
理论上,如果一个传感器能检测到某一段电测波谱发出的能量,我们就可以在这个波段上对感兴趣的事件成像。比较重要的一点要指出,若要使一段电磁波 "看" 到物体,其波长必须小于等于目标的尺寸。
2.3 Image Sensing and Acquisition
我们感兴趣的多数图像是由一个 "光源" 和 被成像的 "场景"(其具有吸收或反射光源能量的元素)组成。加引号是因为其不一定是每天常见的光源和场景,就比如X光照片。
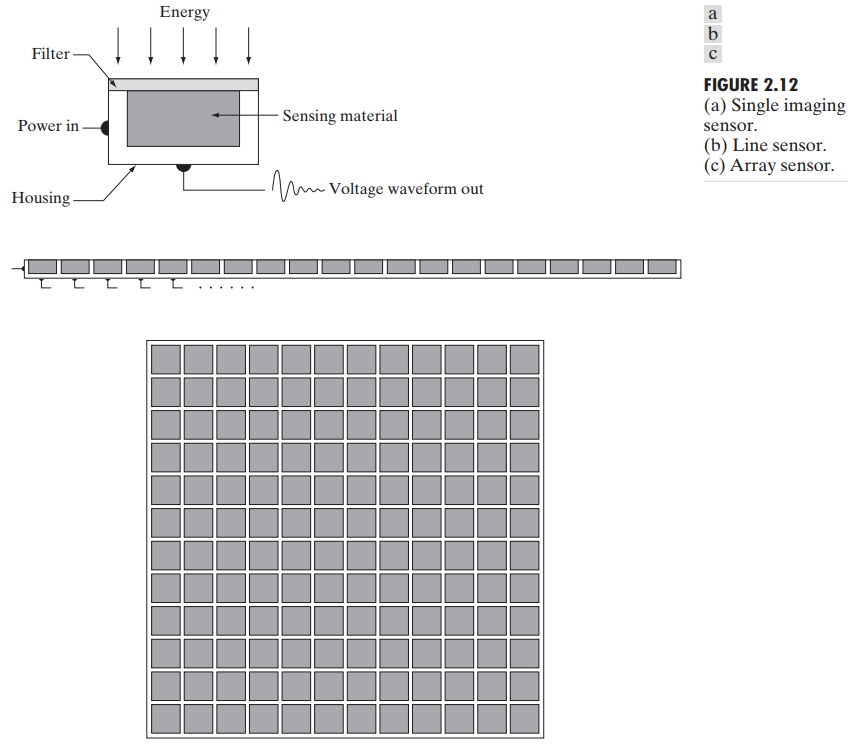
图像传感器原理很简单:入射光通过特定感知材料与输入的电能相结合,转换成电压。输出的电压波形即传感器的响应,而通过把每个传感器的响应数字化,可得到一个数字量,图像数字化将留到 2.4 节讨论。
2.3.1 Image Acquisition Using a Single Sensor
图 2.12(a) 即单个传感器的组件。最常见的这种传感器是光电二极管,其由硅材料制成,输出的电压波形与光强成正比。在传感器的前面使用一个过滤器和提高其光线选择性。
若用这种传感器绘制 2D 图片,就需要给其分别提供在绘制区域上 x 和 y 方向的位移。图 2.13 显示了一个用于高精度扫描的配置。由于机械运动可控精度高,这种廉价而慢速的方法可以得到高精度的图像。另一种配置是在一个平面上,传感器在两个方向上线形移动。这些机械数字化仪有时被称为 microdensitometers(微密度计)。
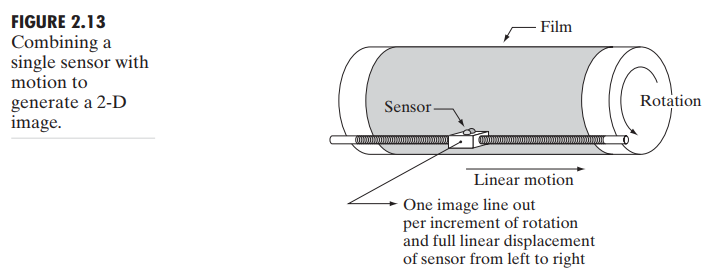
2.3.2 Image Acquisition Using Sensor Strips
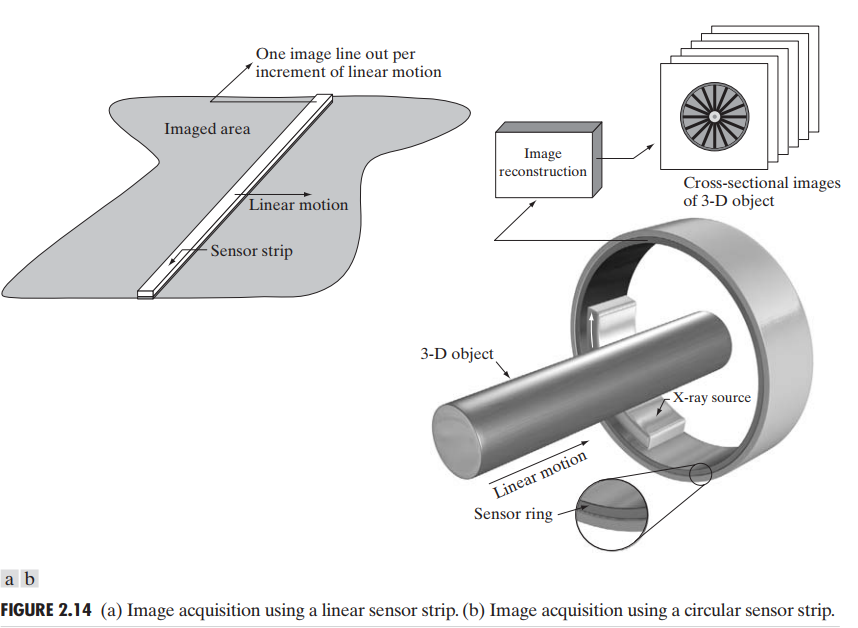
将传感器排成一维直线后组成传感器带,这类几何结构比单个传感器使用更加频繁,如图 2.12(b)。该传感器带在一个方向上提供成像单元,在另一个方向上垂直于传感器带移动而成像,如图 2.14(a)。
以圆环形方式安装的传感器带用于医学和工业成像,以得到 3D 物体的横截面图,如图 2.14(b)。需要注意的是,这类传感器的输出必须通过重构算法以获得有意义的横截面图像,换句话说图像不能直接由传感器获取。
2.3.3 Image Acquisition Using Sensor Arrays
图 2.12(c) 显示了单独的传感器构成了 2D 的传感器阵列。大量电磁波和超声波装置使用这种构造。这也同样是数字摄像机的主要构造方式。这类传感器的主要用法如图 2.15。
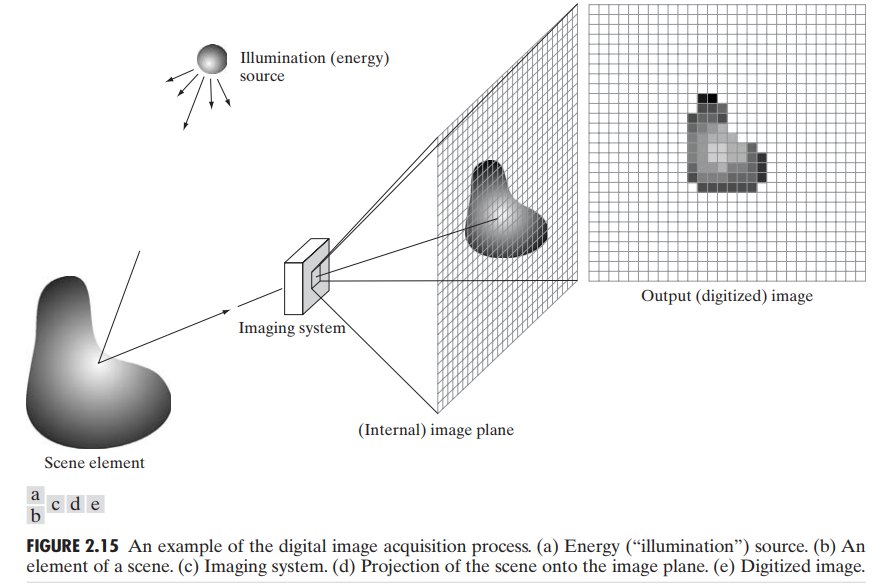
2.3.4 A Simple Image Formation Model
在章节 1.1 中,我们定义了一张图片为形如 $f(x,y)$ 的二元方程。在 $(x,y)$ 处的 $f$ 的值是一个正标量,其物理意义由图片源决定。当一张图片由物理过程产生时,其亮度正比于光源射出的能量,因此,$f(x,y)$ 一定非零值,并且有限:$0<f(x,y)<\infty$。
方程 $f(x,y)$ 可以由两部分组成:
- illumination(反射分量):入射到场景内的光源照射量,记为 $i(x,y)$,其性质取决于光源。
- reflectance(入射分量):被物体反射的光照量,记为$r(x,y)$,其性质取决于成像物体。
$$f(x,y)=i(x,y)r(x,y), 0<i(x,y)<\infty , 0<r(x,y)<1$$
这些表达式也同样适用于入射光通过介质成像(胸透X射线),此时用 transmissivity 替代 reflectance。
设一张单色图的某一点 $(x_0,y_0)$ 的灰度为 $\ell = f(x_0,y_0)$,且$L_{min} \le \ell \le L_{max}$。理论上唯一的要求即 $L_{min}$ 是正数,$L_{max}$ 有限。事实上,$L_{min}=i_{min}r_{min}, L_{max}=i_{max}r_{max}$。区间 $[L_{min},L_{max}]$ 即 gray scale。常见情况是将区间在数字上平移至$[0,L-1]$,$\ell = 0$ 代表黑色,$\ell = L-1$ 代表白色。
2.4 Image Sampling and Quantization
在上一节的讨论中,我们见到了很多种获得图片的方式,不过我们目标都相同:在感知的数据上产生图片。大多数传感器产生的输出都是连续的电压波形,其振幅与空间特性与感知到的物理特点相关。为了产生数字图像,我们需要将这些连续的感知数据转换至数字形式,这包含两个过程:sampling(采样),quantization(量化)。
2.4.1 Basic Concepts in Sampling and Quantization
采样与量化的基本思想如图 2.16。一张图像可能在 x 轴和 y 轴以及振幅上都是连续的。为了将其转化成数字形式,我们需要在其坐标和振幅上分别进行采样,对坐标进行数字化被称为 sampling,对振幅数字化被称为 quantization。
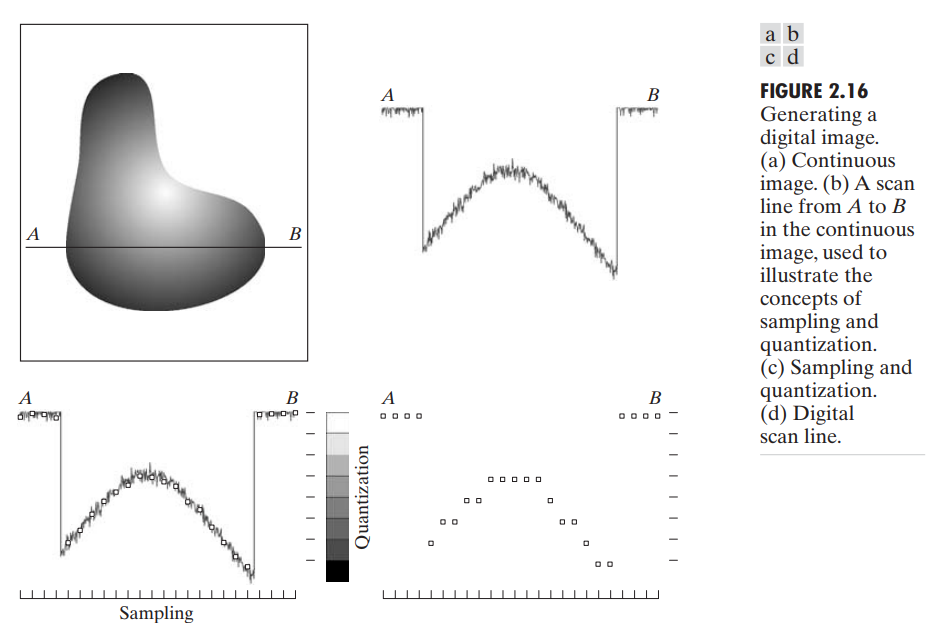
图2.16(c)中白色方块即为对坐标等间隔采样结果,2.16(d)即对振幅量化后的最终数字样本。图中亦可知,量化能达到得精度除了与使用的离散等级得数量相关,也与样本信号得噪声高度相关。
上述采样过程假设了我们有一张在坐标和振幅上都连续的图片,实际上,采样方式由产生图片的传感器的组成决定。当使用单个传感器产生图片时,采样可采用上述过程,具体方式即通过机械位移来使传感器到指定位置采集数据。由于机械运动的高精度,使用这种方式采样可以到达的精度几乎没有限制,但实际上还有其他的干扰因素,比如系统光学原件的数量。
当我们使用 sensing strip 来获得图片,传感器的数目将成为采样精度的限制,虽然我们可以通过机械控制来增加一个方向的精度,但只增加某个方向的精度意义不大。当使用 sensing array 来获得图片时,传感器的个数将成为两个方向的精度限制。
2.4.2 Representing Digital Images
假设我们将一张连续图片采样为二维数组 $f(x,y)$,包含 $M$ 行 $N$ 列,为了简便起见,我们使用这些值作为离散坐标:$x=0,1,2,...,M-1$和$y=0,1,2,...,N-1$,即 0-based。这里的坐标并不代表被采样的图片上的物理坐标系,由一张图像的坐标张成的实平面被称为 spatial domain,而 x,y 被称为 spatial variables 或 spatial coordinates。
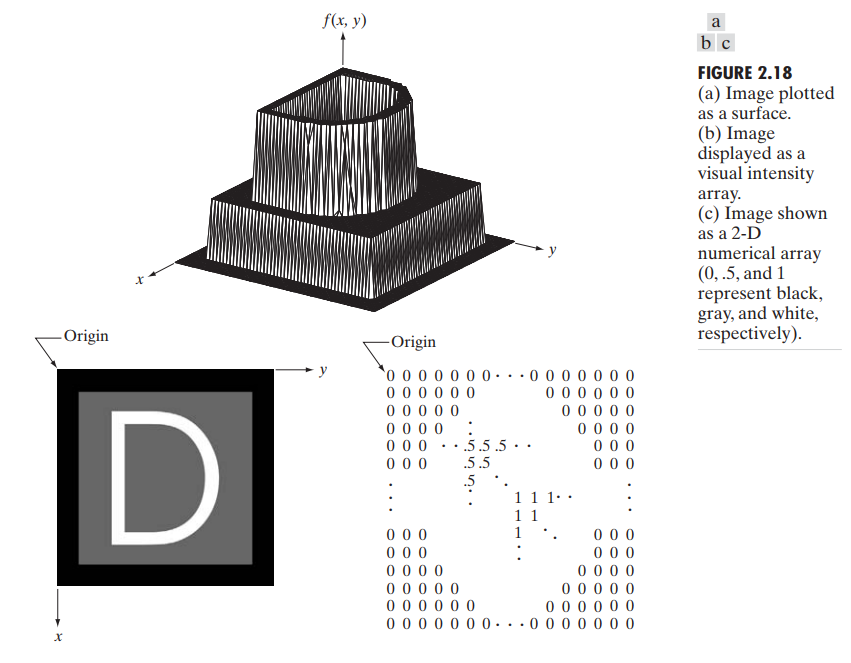
图 2.18 显示了 3 种基本的显示 f(x,y) 的方法。由于复杂图像包含细节过多,很难用图 2.18(a) 来分析,但处理元素为 (x,y,z)三元组时,这种表示还是很有用。通常图 2.18(b) 和图 2.18(c) 更有用。图 2.18(b) 是一个比较一般的表示方法,而图 2.18(c) 是一个矩阵形式,但由于图片大小的关系,通常很难完全打印。
在公式形式上,我们用 $M*N的数值阵列表示,或是以传统矩阵 A$ 表示。矩阵中的每一个元素被称为 image element, picture element, pixel 或 pel。
$$
f(x,y)=
\begin{pmatrix}
f(0,0) & f(0,1) & \cdots & f(0,N-1) \\
f(1,0) & f(1,1) & \cdots & f(1,N-1) \\
\vdots & \vdots & & \vdots \\
f(M-1,0) & f(M-1, 1) & \cdots & f(M-1, N-1)
\end{pmatrix}
= A = \begin{pmatrix}
a_{0,0} & a_{0,1} & \cdots & a_{0,N-1} \\
a_{1,0} & a_{1,1} & \cdots & a_{1,N-1} \\
\vdots & \vdots & & \vdots \\
a_{M-1,0} & a_{M-1, 1} & \cdots & a_{M-1, N-1}
\end{pmatrix}
$$
简要回顾图 2.18,注意数字图像的原点在左上方,x 轴正方向向下,y 轴正方向下右。这种方便的表示法基于一个事实:很多图片显示装置(TV显示器)扫一张图片时是从左上角开始,从左向右扫的。更重要的事实是按照惯例,矩阵的第一个元素在左上角。
数字化过程需要对 M,N 和 L(离散灰度等级)的取值做出决定。除了必须是正整数,对 M,N 没有更多的限制。然而, 由于对存储容量和量化硬件的考虑,灰度等级通常是 2 的幂:L = 2^k。我们假设离散灰度是等间隔的,它们是处于[0,L-1]中的整数。有时候,gray scale 所跨越的值域被非正式德成为 dynamic range。这一术语在不同领域有不同的用法。在这里,我们定义一个图像系统的 dynamic range 为最大可测量灰度和最小可测量灰度的比值。一般来说其上限取决于saturation(饱和度),下限取决于noise(噪声),如图 2.19。

基本上,动态范围确立了系统能表示的最高和最低灰度,这也同样是图片能具有的。与之紧密相关的一个概念是 image contrast(图像对比度),我们定义它为一张图片最高和最低灰度之差。当一张图片中大量像素具有高动态范围时,我们可以预料图片具有高对比度。我们等第3章再讨论这些细节。
存储一张数字图像需要字节为:$b=M*N*k$。当一张图片有$2^k$个灰度等级时,常见的称法是k-bit image。
2.4.3 Spatial and Intensity Resolution
直觉上,spatial resolution 是一张图片中最小可辩别细节的一种度量。在量化上,spatial resolution 可以被表示成好几种方法,其中 line pairs per unit distance 和 dots(pixels) per unit distance 最常用。假设我们用黑白相间的直线带建立一个图,每一条宽 $W units$ ,因此一个 line pair 的宽度为 $2W$, spatial resolution 为 $1/2W$line pairs per unit distance。一个广泛使用的图像分辨率的定义是可分辨的 line pairs per unit distance 的最大数量。在美国,这个测量法通常被表示为 dots per inc (dpi)。空间分辨率的度量必须相对于空间单位来规定才有意义。
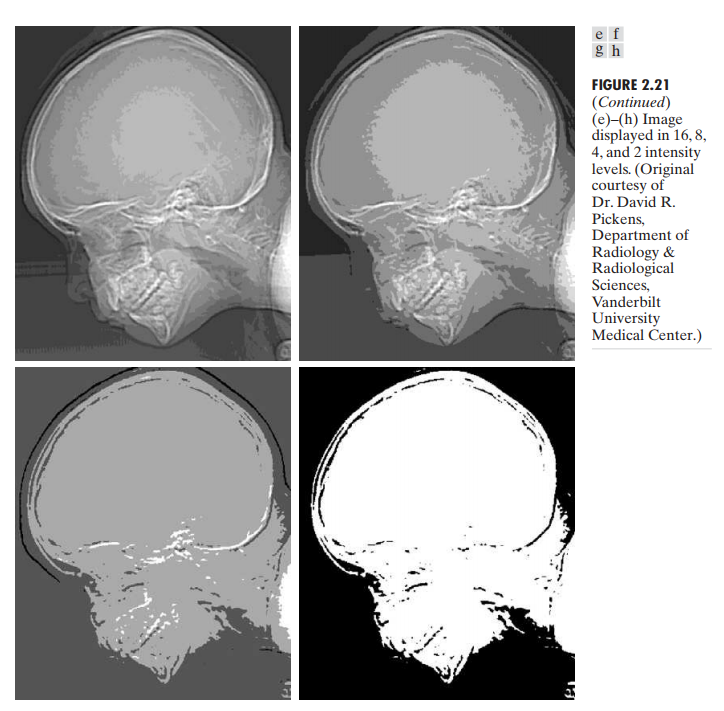
intensity resolution 类似定义为灰度等级上的最小可分辨区别。其通常由硬件决定,一般是 2 的幂。不同于 spatial resolution 必须基于单位距离基础才有意义,常见的做法是将量化灰度需要的字节数视为 intensity resolution,因为可分辨的区别不止受 noise 和 saturation 值影响,还与人类的感知能力相关。
Typical effects of varying the number of intensity levels in a digital image.
false contouring 由在数字图像的平滑地区中使用的灰度等级不足造成。
一个关于同时改变 N 和 k 对图像造成影响的早期研究:图像集合由图 2.2 的三种图像变化 N 和 k 得到,观察者通过主观质量对它们排序

结果被总结为在 NK平面上的 isopreference curves(等偏爱曲线)。坐落在同一条等偏爱曲线的点代表相同主观质量的图片。随着图片中的细节增多,等偏爱曲线趋近于更加垂直。这个结果表示对于有大量细节的图片只需要较少灰度等级。这个结果最有可能的原因是 k 的减小趋向于对比度的明显增加,一个人们通常感受到图像质量改善了的视觉效果。
2.4.4 Image Interpolation
内插是使用在诸如放大、收缩、旋转和几何校正中的基础的工具。我们在这一节中的主要目标是介绍内插并将它应用调整图片大小中,这是基本的图片 resampling 方法。
根本上,interpolation 是使用已知数据去估算未知位置的数据的一个过程。假设一张 $500\times 500 pixels$ 的图像扩大 1.5 倍为 $750\times 750 pixels$。一个简单的放大方法是创建一个 $750\times 750$格的图像,再将其缩小到恰好覆盖原图像。显然 $750\times 750$ 的格子小于原图像的像素格。为了对覆盖的每个点赋以灰度等级,我们将原图上距离其最近的点的灰度赋给它,最后放大至原来大小。
上述方法被称为 nearest neighbor interpolation,因为它将新图上每个点的灰度安排为原图上最近的点。这个方法简单但可能产生不被期望的缺陷,比如直边缘的严重扭曲,因此它很少在实际中使用。一个更适合的方法是 bilinear interpolation ,其中我们用最近的四个邻近点去估算某个位置的灰度值。令 $(x,y)$ 代表新图上的坐标系,$v(x,y)$ 代表其灰度值。则 bilinear interpolation 可被写为:$v(x,y)=ax+by+cxy+d$。四个参数即点 $(x,y)$ 的四个最邻近点。伴随计算负担的适度增长,bilinear interpolation 给出了比 nearest neighbor interpolation 好得多的结果。
下一个复杂度的算法是 bicubic interpolation,它使用了一个点的十六最临近点:$v(x,y)=\sum_{i=0}^{3}\sum_{j=0}^{3}a_{ij}x^iy^j$。
2.5 Some Basic Relationships between Pixels
在这一节里,我们考虑几个重要的数字图像的像素点间的关系。前面提到图像被表示为 $f(x,y)$,在这一节中当我们指一个特定的像素的时候,我们用小写字母表示,例如 p,q。
2.5.1 Neighbors of a Pixel
一个像素点 p 有四个水平和竖直的邻居:$(x+1,y),(x-1,y),(x,y+1),(x,y-1)$。这些点集被称为 p 的 4-neighbors,被称为 $N_4(p)$。四个对角邻居 $(x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1)$被称为 $N_D(p)$。这些点被一起称为 p 的 8-neighbors,$N_8(p)$。当然有一些$N_4(p)$和$N_8(p)$的点可能落在边界外。
2.5.2 Adjacency, Connectivity, Regions, and Boundaries
令 $V$ 为定义邻接性的灰度值集合。在二值图中当我们指值为 1 的像素点间的邻接性时 $V={1}$。在灰度图像中类似,但 $V$ 中包含更多值。我们考虑三种类型的邻接。
- 4-adjacency。当 $q \in N_4(p)$,具有 $V$ 中数值的两像素 p,q 是 4 邻接。
- 8-adjacency。当 $q \in N_8(p)$,具有 $V$ 中数值的两像素 p,q 是 8 邻接。
- m-adjacency。当 $q \in N_4(p)$ 或 $q \in N_D(p)$ 且 $N_4(p)\cap N_4(q)$中的像素点的值都不属于$V$,具有 $V$ 中数值的两像素 p,q 是 m 邻接。
图 2.25 (a)(b)(c)显示了三者的不同。

一条从像素 p 到像素 q 的路径是一系列两两邻接的不同像素点:$(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$。
令 $S$ 表示某张图像中像素点的集合。$S$ 中两像素点 p 和 q 被称为 connected,仅当存在一条完全由 $S$ 中像素点构成的路径。对任意 $S$ 中的 p,与它相连的 $S$ 的像素子集被称为 connected component。如果 $S$只有一个 connected component,则它被称为 connected set。
令 $R$ 为某张图片的像素子集。若 $R$ 为 connected set,我们称它为图片的 region。两 region 相连若它们的合集是 connected set。图2.25(c)(d)(e)是三中不同的邻接方式。
假设一张图片包含 K 个不邻接的 region,令 $R_u$ 代表所有 region 的集合,$(R_u)^c$ 代表其补集。我们称 $R_u$ 中的点为 foreground,$(R_u)^c$ 是图片的 background。